2025.01.08 - Lecture 2

$|K|={\cup }_{\sigma \in K}\sigma$ (body of $K$). The body of each geometrical simplicial compact is a compact subset of $R^d$.

Definition. Sub-complex $L$ of $K$
A Sub-complex $L$ of $K$ is a complex s.t. if $\sigma \in L$ then $\sigma \in K$ ($L\le K$).

Definition. $j$-skeleton of $K$
The $j$-skeleton of $K$ is a collection of all simplexes of $K$ having dimension less than or equal to $j$.

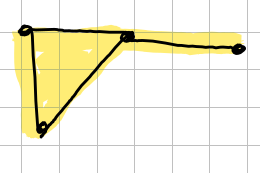
The $1$-skeleton is the set of simplexes of dimension less than 1, so are the segments, the points and the empty set.

Abstract Simplicial Complex

It is a finite collection $A$, with $A\ne \{\varnothing \}$ and $A=\{{\alpha }_i{\}}_{i\in I}$ with $a_i\subseteq {\mathbb{R}}^d$ verifying:

$$\beta \subseteq \alpha \in A⟹\beta \in A$$

with a finite $I$.
Each set in $A$ is finite.

Note. The second property of the geometrical simplicial complex holds here, but it’s free we don’t need to set it.

$${\alpha }_1,{\alpha }_2\in A$$ $${\alpha }_{}\cap {\alpha }_2\le {\alpha }_1$$ $${\alpha }_1\cap {\alpha }_2\le {\alpha }_2$$

We have a finite collection and each subset belongs to the collection, and since it’s finite we can’t have elements of $A$ that are infinite.
In $A$ for every set in it, we also have all subsets.
e.g.

$$A=\{\varnothing ,\{Alice\},\{Paul\},\{Bob\},\{Alice,Bob\},\{Alice,Paul\},\{Paul,Bob\}\}$$

Isomorphism between $A$ and $B$

$A$ and $B$ are a.s.c.
With $\varphi$ being the bijection:

$$\varphi :vert(A)\to vert(B)$$ $$\alpha \in A⟹\varphi (\alpha )\in B$$ $$\beta \in B⟹{\varphi }^{-1}(\beta )\in A$$

A trivial example of isomorphism is the $\varphi :B\to B$, in general, when we can translate the vertice of an a.s.c. to the vertices of another a.s.c. bijectively we have isomorphism between the two.

Relations between g.s.c. and a.s.c.

Let $K$ be a g.s.c., we can immediately get an a.s.c. by defining the vertex scheme of $K$, denoted as $Ab(K)$, as the following:

$$Ab(K)=\{\{u_0,...,u_k\}|<u_0,...,u_k>\in K\}$$

N.B.: $<u_0,...,u_k>$ is a convex hull $\in K$.

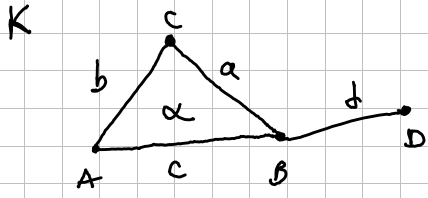
In this specific case, $Ab(K)$ is equal to:

$Ab(K)=\{\varnothing ,\{A\},\{B\},\{C\},\{D\},\{A,B\},\{A,C\},\{B,C\},\{B,D\},\{A,B,C\}\}$

It’s possible to get from a a.s.c. to a g.s.c. ?
Yes, by using the Geometric realization theorem.

Geometrical realization theorem

We say that the g.s.c. $K$ realizes the a.s.c. $B$ iff:

$$B\cong Ab(K)$$

B is isomorphic to the vertex scheme of $K$.

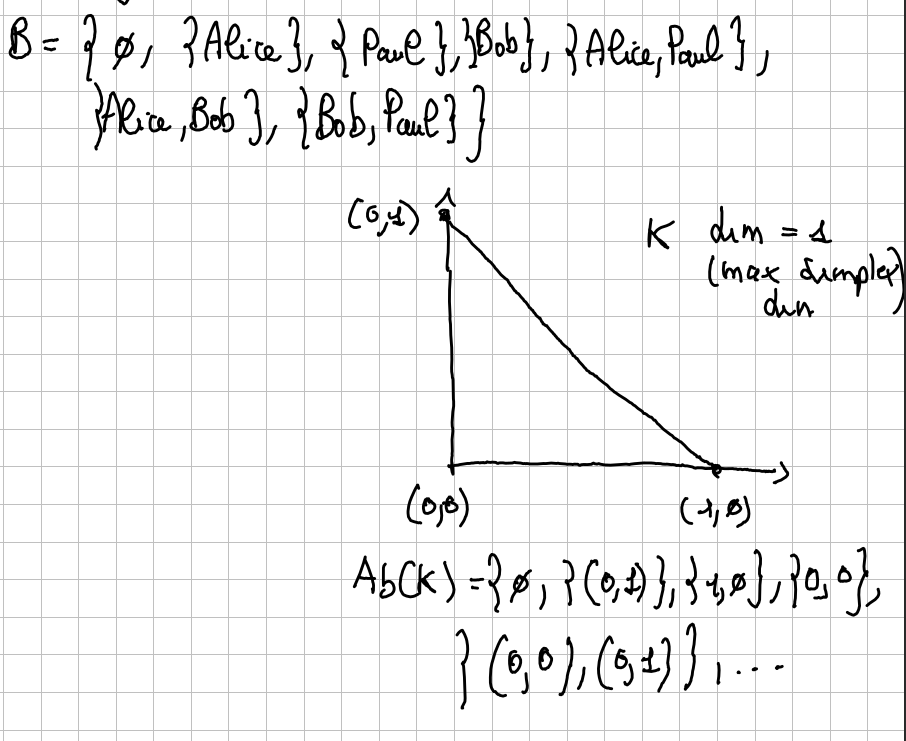
It’s isomorphic because you can assign to each element of $B$ one of $Ab(K)$ and the opposite. A.k.a you can go from the view with coordinates and points, to the textual one by assigning to each point one of the names (Alice, Bob and Paul).

Theorem: Geometric Realization Theorem Let $B$ be a a.s.c. of dimension $d$. $B$ can be realized as a g.s.c. $K$ in ${\mathbb{R}}^{d+1}$.

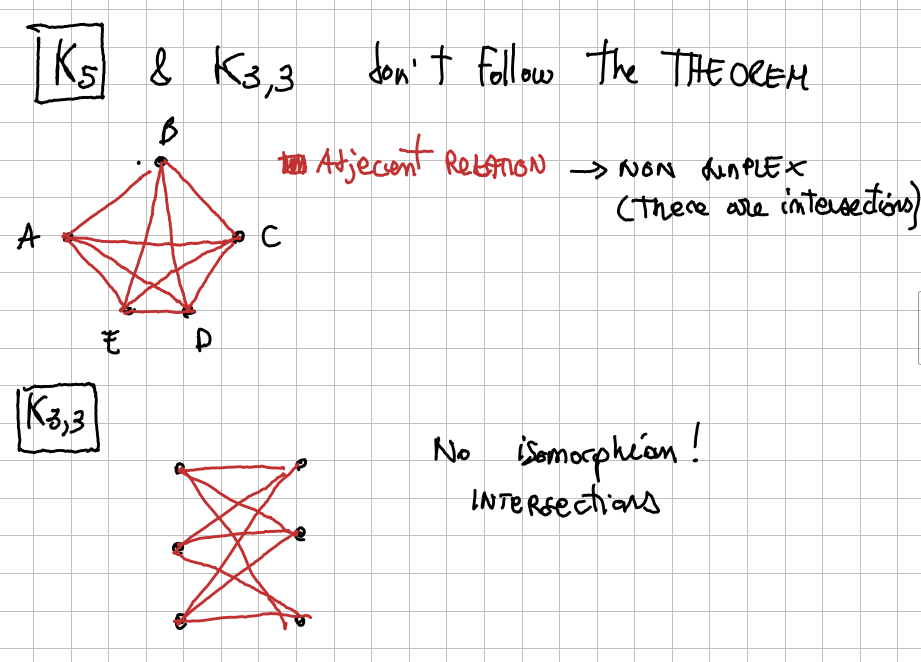
If you take the graph $K_5$ and the adjacency are by the line drawn in red. The red part is just the structure. This is not realizable in ${\mathbb{R}}^2$, it’s easy to do in ${\mathbb{R}}^3$. So you can’t do better than the theorem, in the sense that you need all those dimensions.

Nerve

Definition of Nerve. Let us assume to have a finite collection $F$ of open sets:

$$F=\{x_i{\}}_{i_{\in }I}(x_i\subseteq Y)$$

With a finite $I$.

We call Nerve, $NrvF$, the collection of all the subsets of $F$ having non-empty intersection.

$$\{x_i\}j\le i|{\cap }_{x_i}\ne \varnothing$$

$F=\{x_1,x_2,x_3\}$

$$NrvF=\{\{x_1,x_2\},\{x_1,x_3\},\{x_2,x_3\},\{x_1,x_2,x_3\},\{x_1\},\{x_2\},\{x_3\},\{\varnothing \}\}$$

The empty set is there, because the intersection of a family of empty set is not empty.

How to transform a cloud of points in ${\mathbb{R}}^d$ into a g.s.c. ?

There are plenty of methods to do it, we are going to see the Čech complex and the Vietoris-Rips Complex.

Čech complex

Let us assume that $S\subseteq {\mathbb{R}}^d$ that is finite. Let us choose a $r\ge 0$.
Set $F=\{B(x,r):x\in S\}$.
$B$ is the ball centered in $x$ with radius $r$.

We then consider the $NrvF$.

$NrvF=\{\varnothing ,\{B(x_1,r)\},\{B(x_2,r)\},\{B(x_3,r)\},\{B(x_1,r),B(x_2,r)\},\{B(x_2,r),B(x_3,r)\},\{B(x_1,r),B(x_3,r)\},\{B(x_1,r),B(x_2,r),B(x_3,r)\}\}$
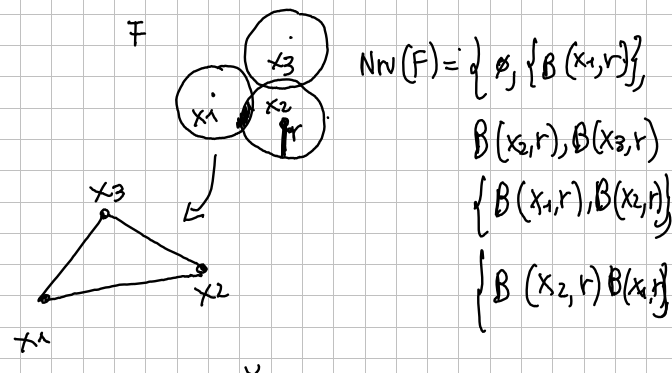
We can than realize the g.s.c. from the $Nrv$.
$NrvF$ is called Čech complex of $S$ with radius $r$.

Vietoris-Rips Complex

$S=\{x_1,...,x_n\}$, $r\ge 0$
The Vietoris-Rips is:

$$VR(S,r)=\{\text{subsets of }S\text{ having diameter }\le 2r\}$$

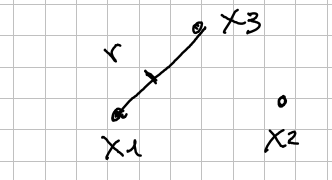
The evolution of the a.s.c. when you increase $r$ is just the three singletons, then when your reach $r=1/2\delta$ where $\delta$ is the distance between the points, the segments starts to join the a.s.c.

Vietoris-Rips Lemma. When you take the $\widehat{\check{C}ech(s,r)}\subseteq VR(S,r)\subseteq \widehat{\check{C}ech(s,\sqrt{2}r)}$

The $\widehat{......}$ operator is used to consider the center of the ball.

Collapsibility

We have a g.s.c. $K$:

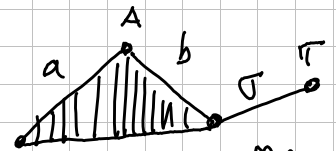
If there is some simplex with just a co-face: We can consider the new complex $L^{\prime }$ obtained from $K$ by removing $\tau$ and $\sigma$. We say that we can collapse $\tau$.

Co-Face

If $\tau$ is a face of $\sigma$, then $\sigma$ is a proper co-face of $\tau$.

In the image $\tau$ is a face of the edge $\sigma$. We can remove $\tau$ and $\sigma$. This move is called elementary collapse. The inverse is adding them again. Called inverse elementary collapse.

Applying it sequentially, to the image you can remove it until you have just one point.

Let’s see the procedure:

1. We remove $\tau$ and $\sigma$;
2. Then, since each edge it’s the only co-face of the triangle $R$, we can remove one of it, alongside the triangle;
3. Then, we procede to remove $C$ and $c$ since $c$ it’s the only co-face of $C$;
4. Finally, we do the same for the other point $B$ and its co-face $b$;
5. We obtain just the single point $A$.

When this happens, the complex is called collapsible.

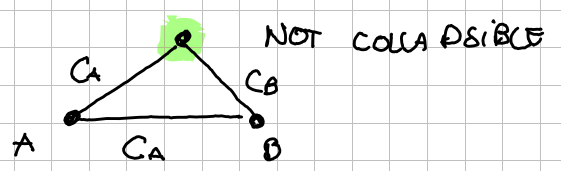
Example of a non-collapsible simplicial complex:

Defition of the elementary space ${\mathbb{Z}}_2$

${\mathbb{Z}}_2=\{0,1\}$ with just the two operations $({\mathbb{Z}}_2,+,\cdot )$.

Definition of Quotient Space.
Let $V$ be a vector space. Assume that $W$ is a vector sub-space of $V$ $(W\subseteq V)$.

$$\frac{V}{W}$$

Chain Complex

Chain complex is a sequence of vector spaces

$$\mathcal{C}=...,V_{P+1},V_P,V_{P+1},V_{P+2},...$$

$v_{p+1}$ is the homorphism between the vector spaces.

$$v_p\circ v_{p+1}\cong 0$$

Definition of Kernel, Image and Homology of a Chain Complex
$ker{v}_p=$ set of $p$-cycles
$Im{v}_{p+1}=$ set of $p$-boundaries

$$\frac{ker{v}_p}{Im{v}_{p+1}}=H_p(\mathcal{C})$$

Homology group of the chain complex $\mathcal{C}$ in degree $p$

$$\text{Im }{v}_{p+1}\subseteq \text{ker }{v}_p⟹v_{p+1}(u)\in \text{ker }{v}_p(v_{p+1}(u)=\varnothing )$$

Formal Linear Combination

$$X=\{x_i{\}}_{i\in I}\text{ with }{a}_i\text{ taken from }\mathbb{Z}\text{, i.e}{a}_i\in {\mathbb{Z}}_2$$ $$\sum _{i\in 0,...,n}{a}_i{x}_i$$

Short-manner formal way of representing a subset of $X$, i.e. of choosing some $x_i$.