2025.01.08 - Lecture 1

What is the shape of data? Not a trivial problems, we can use some tools:

1. Geometric simplicial complexes: It is the joining of points, segments and figures in any dimensions.
2. Homology groups: Algebraic tool that describe holes in a simplicial complex.
3. The natural pseudo-distance: is used to compare data under the action of a group.

Persistence Diagrams

Imagine you have a function between (0,1) and you have a discretization of the interval.
And you have a function $\varphi$ from this interval to itself.

$\varphi (0)=0.2$
$\varphi (0.2)=0.6$
etc.

The lines are there for the explanation (between points, since it’s discretized).

The question is what is the shape of the function. How to represent it’s shape mathematically?

We take a level $t$ and we consider the sub-level set which is the set of points where the function $\varphi$ takes a value that it’s less than $t$.
The idea is counting the number of components when changing $t$, going from $-\inf$ to $+\inf$.

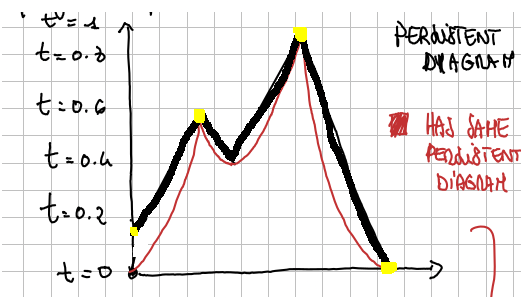
We take a low $t$ and we increase it’s value until there is the birth of a component, it enters the sub-level set. Each point it’s described by it’s time of birth, on the left of the pair, and the time of death, on the right, so we have:

$(0,\inf )$
$(0.2,1)$
$(0.4,0.6)$

The construction of this list happens like this:

1. at $t<0$ we have no components;
2. at $t=0$ a component join, the one with $x=1$. So we add a $(0,$ to the list;
3. at $t=0.2$ a second component joins we add a $(0.2,$ to the list;
4. at $t=0.4$ a new component, the one with $x=0.4$ joins the collection, so we write $(0.4$ in the list;
5. at $t=0.6$ the two points, the one that joined at $t=0.2$ and $t=0.4$ become contiguous, so by definition the younger one dies, and we add the $t$ of death to $0.4$ by writing in the list $(0.4,0.6)$;
6. at $t=1$ the first point, that joined at $t=0$ and the rest of the joined points, represented by the oldest one, the one that joined at $t=0.2$ are contiguous, so the youngest one dies and we add the $t$ of death by writing $(0.2,1)$ to the list.
7. Finally, all the function is contiguous and changing $t$ will do nothing, so we add the time of death to the remaining components by writing $(0,\inf )$.

Even if this was not discretized, or you amplify it, the collection of points written on the right doesn’t change, this points are the persistence diagram.

The persistence diagram $Dgm(\varphi )$ contains only six numbers. You lose a lot of information, you can draw an infinite number of function with the same persistence diagram (an example in the picture is the function in red, which has the same diagrams as the one in black). So we lose a lot of information, but for a lot of tasks this information is sufficient, for example in seeing the similarity of the shape.

GENEOs

Group Equivariant Non-Expansive Operators.
The computation of Persistence Diagram is a trivial case of GENEOs.

Blurring and the group of isometrics (rotation) of an image are GENEO, you can apply the two transformation (blurring and isometrics of rotation) in any order and the result is the same. So the two transformation are equivariant. Basically, applying these two operators in any order does not change the distance of the results.

Geometric Simplicial Complexes

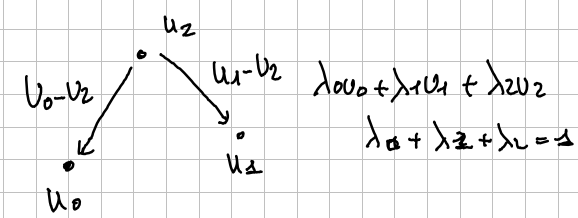
Definition of Affine Combination. The affine combination of the vectors $u_0,...,u_k\in {\mathbb{R}}^d$ with coefficients ${\lambda }_0,...,{\lambda }_k$:

$$\sum _{i=0}^k{\lambda }_i{u}_i$$

Under the assumption that ${\sum }_{i=0}^k{\lambda }_i=1$

If I have two points $u_0$ and $u_1$ we can say that ${\lambda }_0+{\lambda }_1=1$ which means that the linear combination can be written as ${\lambda }_0{u}_0+(1-{\lambda }_0)u_1$, with ${\lambda }_0\in \mathbb{R}$.

We consider the real lines that unites the two points.

If we do the same with three points

$${\lambda }_0{u}_o+{\lambda }_1{u}_{}+{\lambda }_2{u}_2$$

With:

$${\lambda }_0+{\lambda }_1+{\lambda }_2=1$$

We are considering the plane contained by the three points.

The set of any affine combination of the points $u_0,...,u_k\in \mathbb{R}$ you get the affine hull of $u_0,...,u_k$.

We are considering point in general position. But let’s consider taking three points belonging on the same line (not general position).
In the general case the affine hull of three points is a plane, but in this case is a line (but can also be a point if they are all in the same position).

To free the definition from this case, we assume that our points $u_0,...,u_k$ are affinely independent.

Definition of affinely independence.

$$\sum {\lambda }_i{u}_i=\sum u_i{u}_i$$

and

$$\sum {\lambda }_i=1\text{ or }\sum u_i=1$$

Then:

$$\forall i{\lambda }_i=u_i$$

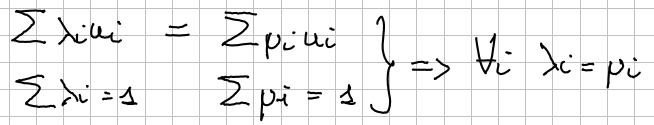
The points $u_0,...,u_k$ are affinely independent if and only if the vectors $u_1-u_0,u_2-u_0,u_k-u_0$ are linearly independent.

You can just consider the vectors that connect each point to another are linearly independent.

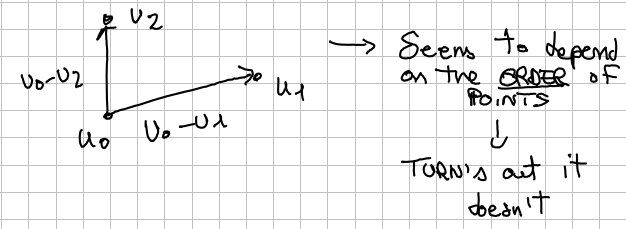
You get the same result if you consider another starting point for the vectors.

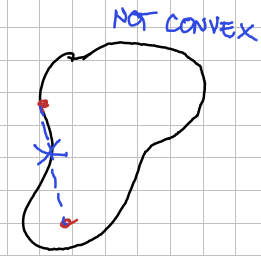
Convex Set

Considering a subset of a vector space, we say it’s a convex set if every point inside it are connected by a segment contained in the subset.

Definition of Convex Set. A subset $S\subseteq {\mathbb{R}}^d$ is convex if $\forall x_1,x_2\in S,\forall \lambda \in [0,1]$ we have that $(1-\lambda )x_1+\lambda x_2\in S$.

Compact Set

In ${\mathbb{R}}^d$ compact sets are set that have the following properties:

1. They are close. A set is closed if it contains its border. So $[0,1]$ in $\mathbb{R}$ is closed because it contains bot its boundaries, $0$ and $1$, while $(0,1)$ its open.
2. They are bounded. A set $S\subseteq {\mathbb{R}}^d$ is bounded if there exists a real number $M>0$ such that the distance between any points in $S$ is less than $M$. A.k.a. if $S$ can be contained in a sphere of finite radius.

Each compact set $C\subseteq {\mathbb{R}}^d$ has this property: if $\{U_i{\}}_{i\in I}$ is an infinite family of open subsets of $\mathbb{R}$ such that $C\subseteq {\cup }_{i\in I}{U}_i$, then a finite subfamily $\{U_{i1},...,U_{ik}\}$ exists, such that $C\subseteq {\cup }_{r=1}^k{U}_{ir}$.

So, basically, if a infinite family of open subsets of $\mathbb{R}$ contains $C$ then exists a finite subfamily of that family that also contains $C$.

Convex combination

Definition of Convex combination Convex combination of ${\sum }_{i=0}^k\lambda U_i$ is an affine combination where all coefficient ${\lambda }_i$ are non-negative.

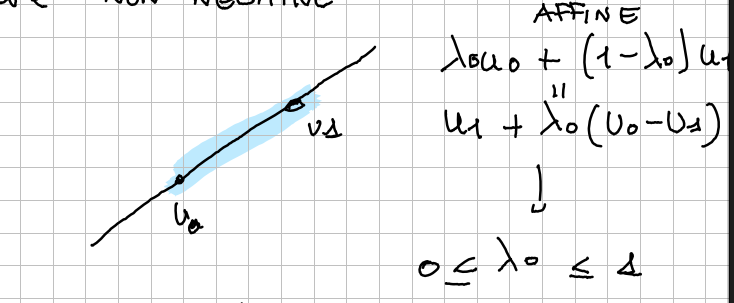
Affine combination means

$${\lambda }_0{U}_o+(1-{\lambda }_0)U_1=U_1+{\lambda }_0(U_0-U_1)$$

To have both non-zero, it meas that

$$0\le {\lambda }_0\le 1$$

We are considering just the points between the two $U_0$ and $U_1$.

If we consider three points in general position we get a triangle.

If we consider four points in general position we get a tetrahedron.

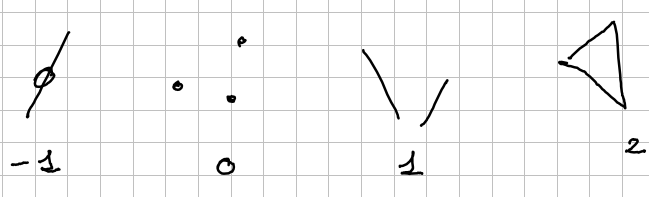
Simplex

Definition of a k-Simplex. A k-Simplex is the convex hull of k+1 points $u_0,...,u_k$ that are affinely independent.

a 0-Simplex is a point, a 1-Simplex is a line, and so on.
The empty set is the unique Simplex in dimension -1.

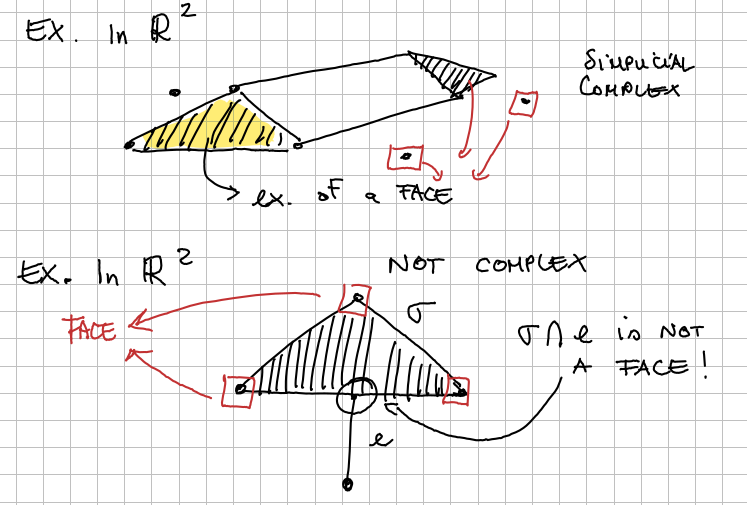
Simplicial Complex

Definition of Geometrical Simplicial Complex. A geometrical Simplicial Complex is a collection $K$ of simplexes $i\in {\mathbb{R}}^d$, verifying these two properties:

$$\text{1) }\sigma \in K,\tau \le \sigma \text{ then }\tau \in K$$

$\tau \le \sigma \text{ is read as }\tau \text{ is a face of }\sigma$ *.

For each simplex we have many faces, in the triangle we have 3 face of 1 dimension (the segments) and three faces of 0 dimensions (the points) and the empty set as the face in the dimension -1.
The first property requires that the collection of simplex must verify that if $\sigma$ belong to K and tau is a face of sigma, than tau must belong to K. If you put a simplex in the collection you also have to put all the faces.

$$\text{2) }{\sigma }_1,{\sigma }_2\in K\text{ then }{\sigma }_1\cap {\sigma }_2\in K.$$

and ${\sigma }_1\cap {\sigma }_2$ is both a face of ${\sigma }_1$ and a face of ${\sigma }_2$, so

$${\sigma }_1,{\sigma }_2\in K\text{ then }{\sigma }_1\cap {\sigma }_2\le {\sigma }_1\text{ and }{\sigma }_1\cap {\sigma }_2\le {\sigma }_2$$