2025.02.06 - Lecture 2

Fuzzy Logic

Fuzzy sets are a type of set where membership cannot be established with certainty but trough a continuous function.

Different types of Uncertainty

Uncertainty analysis in Machine Learning begins with the formal definition of the uncertain quantities involved in the modelling problem.

Aleatoric uncertainty can’t be reduced while epistemic can be reduced.

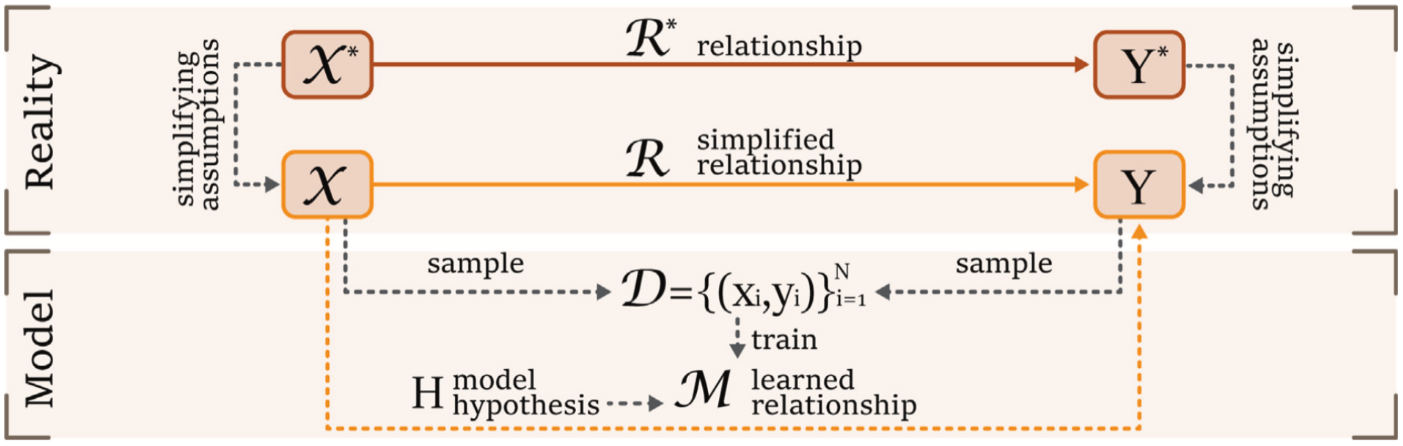
The goal of the mathematical modeling process is to estimate the relationship $R$ using an approximating model $M$ constructed from a dataset $D$ and as et of hypothesis $H$.

Approximating model:

$$M:=M_h=M_{\theta ,\hat{h}}=\mathcal{X}\to \mathcal{Y}$$

Sample of inputs and associated values:

$$D=\{({\mathbf{x}}_i,y_i){\}}_{i=1}^n\subset \mathcal{X}\times \mathcal{Y}$$

Set of trainable and non-trainable parameters:

$$h=(\theta ,\hat{h})\in H$$

Aleatoric Inherent Uncertainty

$\mathcal{R}$ is usually not deterministic, and the source of uncertainty is a property of the relationship/reality and thus can’t be reduced by providing more data or improving the models. The Aleatoric Inherent Uncertainty can be considered a function of both the input $x$ and the relationship $\mathcal{R}$:

$$x\to \mathcal{R}(x)+{ϵ}_{A,I},\text{ where }{ϵ}_{A,I}:={ϵ}_{A,I}(\mathbf{x},\mathcal{R})$$

Contains randomness, we can’t do nothing about it.
Example: Consider a relationship $R$ which associates an integer $x$ with the value given by the sum of $n$ six-sided dice. $R$ is inherently random, since the same input $x$ may correspond to different outputs $y$.

Aleatoric Experimental Uncertainty (or Noise)

It refers to the variations in information content caused by the acquisition process like artifacts, errors in labels, measurements errors, experimental settings, etc.

This uncertainty affects both the input and output, making the problem almost mathematically intractable. But i is possible to change the perspective of the problem:

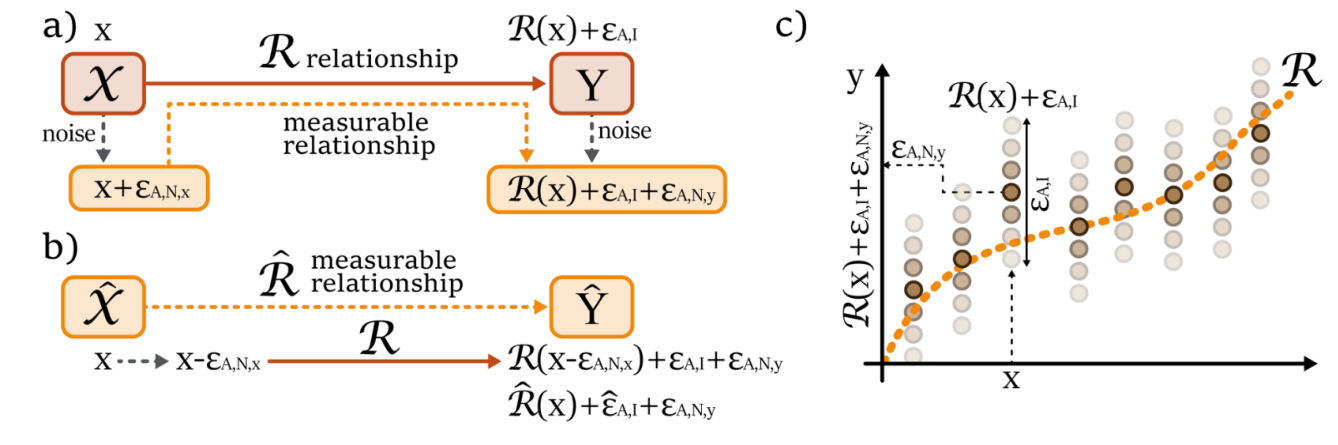
The original would be:

$$\mathcal{X}+{ϵ}_{A,N,\mathbf{x}}\to \mathcal{R}(x)+{ϵ}_{A,I}(\mathbf{x},\mathcal{R})+{ϵ}_{A,N,y}$$

the shift would be:

$$\mathcal{X}+{ϵ}_{A,N,\mathbf{x}}\to \mathcal{R}(x)+{ϵ}_{A,I}+{ϵ}_{A,N,y}:=\hat{\mathcal{R}}(\mathbf{x})={ϵ}_{A,I}(\mathbf{x},\hat{\mathcal{R}})+{ϵ}_{A,N,y}$$

e.g.
We use two rulers each have it’s own uncertainty. We assume the first measure is exact, all the error is translated in the second measurement, plus the error propagation of the first.

Aleatoric Model Uncertainty

Aleatoric uncertainty can also be generated by the model $\mathcal{M}$ during the inference process. This is due to the pseudo-random propagation of rounding errors on a machine.

Aleatoric Model Uncertainty (${ϵ}_{A,M}$) is often negligible compared to the other components of aleatoric uncertainty. We will consider only the inherent and the noise.

Epistemic Uncertainty

Epistemic Uncertainty can also be called subjective, reducible or systematic.

Can be induced by the a priori choice of hyper-parameters characterizing the model or by a finite amount of available data.

Since this uncertainty is due to a lack of knowledge it can be reduced by improving the model hyper-parameters or by increasing the size of the dataset (i.e. it’s the reducible part of total uncertainty)

The approximated model is

$$\mathcal{M}:={\mathcal{M}}_h={\mathcal{M}}_{\theta ,\hat{h}}:\mathcal{X}\to \mathcal{Y}$$

$\mathcal{X}$ and $\mathcal{Y}$ are the representation of the whole space. We are assuming to train with infinite data.

We focus on the model’s parameters, we have $\theta$ which are the trainable parameters (weights and biases), and $\hat{h}$ which are the non-trainable parameters, like which model we are using, the model’s geometry, the loss function, and other hyper-parameters.

We fix hyper-parameters $\hat{h}$, we have to choose the optimal $\mathcal{M}$ which is fully characterized by its trainable parameters $\theta$.

We want to find $\theta \ast$ which is the one that minimize the loss. Formalizing the problem:

$$\theta \ast :\arg \min {\mathbb{E}}_l(\theta ,\hat{h})\to$$ $${\mathbb{E}}_l(\theta ,\hat{h}):={\int }_{\mathcal{X}\times \mathcal{Y}}l({\mathcal{M}}_{\theta ,\hat{h}},y)p(x,y)d\mathbf{x}dy$$

we obtain the optimal bayesian predictor:

$${\mathcal{M}}_{{\theta }^{\ast },\hat{h}}$$

with fixed, established hyper-parameters and optimal trainable parameters.

Even with optimal trainable parameters and even assuming a null aleatoric uncertainty (inherent + noise) ${ϵ}_A$ there could be a discrepancy between the optimal reality and the model outcome: $\mathcal{R}(x)\ne {\mathcal{M}}_{{\theta }^{\ast },\hat{h}}(x)$.
The discrepancy between the Optimal Bayesian Predictor and the reality is called Epistemic Model Uncertainty$({ϵ}_{E,M})$:

$${\mathcal{M}}_{{\theta }^{\ast },\hat{h}}=\mathcal{R}(x)+{ϵ}_{E,M}$$

even with an infinite amount of data, when you project some amount of information in the problem (you choose a structure, you choose a loss function, etc.), you will always approximate the reality. You will never reach the reality. Thus, the ${ϵ}_{E,M}$ can be reducible, but cannot be deleted.

So the Optimal Bayesian Predictor is the best approximation of reality we can get.

Epistemic Approximation Uncertainty

The approximating model $\mathcal{M}$ requires full knowledge of the space $\mathcal{X}\times \mathcal{Y}$, which is usually not available to the experiments and we have to use a dataset. Information about the space $\mathcal{X}\times \mathcal{Y}$ is provided by a sample called $D$, the training dataset:

$$D=\{({\mathbf{x}}_i,y_i){\}}_{i=1}^n\subset \mathcal{X}\times \mathcal{Y}$$

Once the hyper-parameters $\hat{h}$ are established , the goal is to induce an optimal trainable parameters $\hat{\theta }$ on dataset $D$.

$$\hat{\theta }:=argmin{\hat{\mathbb{E}}}_l(\theta ,\hat{h})\approx {\theta }^{\ast }$$

$\hat{\theta }$ is the approximation of optimal trainable parameters. Which are obtained trough the minimization of the loss/risk:.

$\hat{\theta }$ is an approximation of ${\theta }^{\ast }$. The discrepancy depend on the quality and the number $N$ of data available and is called the Epistemic Approximation Uncertainty (${ϵ}_{E,A_p}$):

$${\mathcal{M}}_{\hat{\theta },\hat{h}}={\mathcal{M}}_{{\theta }^{\ast },\hat{h}}+{ϵ}_{E,A_p}$$

We obtain an empirical model

$${\mathcal{M}}_{\hat{\theta },\hat{h}}$$

where the trainable parameters are the best one obtainable on your data-set $\mathcal{D}$.
The discrepancy between ${\theta }^{\ast }$ and $\hat{\theta }$ depends on the quality and the number $N$ of data available and is called the Epistemic approximation Uncertainty(${ϵ}_{E,A_p}$)

$${\mathcal{M}}_{\hat{\theta },\hat{h}}={\mathcal{M}}_{{\theta }^{\ast },\hat{h}}(x)+{ϵ}_{E,A_p}$$

This is also called interpolation uncertainty and can be reduced by improving quality and size of the dataset.

Balancing Epistemic Uncertainty

The empirical distribution $p(\mathcal{D})$ obtained from $\mathcal{D}$ and used to train the model, imperfectly mimics the real underlying distribution on $\mathcal{X}\times \mathcal{Y}$ (i.e. $p(\mathcal{D})\approx p(\mathcal{X}\times \mathcal{Y}$ )

Increasing the dataset size $N\to inf$ improves the approximation, reducing the Epistemic Approximation Uncertainty ${ϵ}_{E,A_p}\to 0$ but cannot reduce the epistemic model uncertainty.

Increasing the complexity of the model (increasing the number of trainable parameters $\theta$) improves the model’s ability to approximate a deterministic relationship $\mathcal{R}$.

For ANN, the Universal Approximation Theorem ensures that a sufficiently complex Neural Network can perfectly approximate every relationship $\mathcal{R}({ϵ}_{E,M}\to 0)$.

However the increasing complexity requires a huge amount of data to be trained on, resulting in a dramatic increase in Epistemic Approximation Uncertainty $({ϵ}_{E,A_p}\to inf)$.

Summary of the uncertainties

$$y=\mathcal{R}(\mathbf{x})+{ϵ}_{A,I}+{ϵ}_{A,N}$$

Here $\mathcal{R}$ is the representation of reality that we would like to reach. It’s always affected by the inherent aleatoric uncertainty and the noise. This are non-reducible

$${\mathcal{M}}_{{\theta }^{\ast },\hat{h}}(\mathbf{x})\approx y+{ϵ}_{E,M}$$

Here, we have the epistemic model uncertainty that is related to the choice of the model by fixing hyper-parameters, geometry etc. However, by having an infinite amount of data we find the optimal bayesian predictor, which has the best set of trainable parameters.

$${\mathcal{M}}_{\hat{\theta },\hat{h}}\approx {\mathcal{M}}_{{\theta }^{\ast },\hat{h}}(\mathbf{x})+{ϵ}_{E,A_p}$$

And here we also have the “problem” of the amount of data, because we can only train our model with sampling from reality. (Epistemic Approximation Uncertainty)

2. The optimal bayesian predictor is the best approximation of R on the whole space
3. Empirical model best approximation of predictor on the dataset D.

The equation that contains the full relationship between the actual model and the reality can be summarized as:

$${\mathcal{M}}_{\hat{\theta },\hat{h}}(\mathbf{x})\approx \mathcal{R}(\mathbf{x})+{ϵ}_{A,I}+{ϵ}_{A,N}+{ϵ}_{E,M}+ϵE,A_p:=\mathcal{R}(\mathbf{x})+{ϵ}_A+{ϵ}_E$$

Can be summarized in the sum of the aleatoric uncertainty and the epistemic uncertainty (predictive posterior uncertainty). However uncertainties are not additive terms, because they must be considered as nonlinear functions, so they also have a multiplicative component. Our aim is to reduce uncertainty.

Techniques to handle Uncertainty

Are divided in:

1. Intrusive (By design);
   • complex implementation;
   • computationally expensive;
   • effective;
2. Semi-Intrusive;
   • effective and easy to implement;
   • computationally expensive;
3. Non-Intrusive (Post-hoc);
   • easy implementation;
   • computationally less expensive;
   • inferior performances;